[NDSS'19] Send Hardest Problems My Way: Probabilistic Path Prioritization for Hybrid Fuzzing

Posted on Edited on

Abstract

Hybrid fuzzing which combines fuzzing and concolic execution has become an advanced technique for software vulnerability detection. Based on the observation that fuzzing and concolic execution are complementary in nature, the state-of-theart hybrid fuzzing systems deploy “demand launch” and “optimal switch” strategies. Although these ideas sound intriguing, we point out several fundamental limitations in them, due to oversimplified assumptions. We then propose a novel “discriminative dispatch” strategy to better utilize the capability of concolic execution. We design a Monte Carlo based probabilistic path prioritization model to quantify each path’s difficulty and prioritize them for concolic execution. This model treats fuzzing as a random sampling process. It calculates each path’s probability based on the sampling information. Finally, our model prioritizes and assigns the most difficult paths to concolic execution. We implement a prototype system DigFuzz and evaluate our system with two representative datasets. Results show that the concolic execution in DigFuzz outperforms than those in state-of-the-art hybrid fuzzing systems in every major aspect. In particular, the concolic execution in DigFuzz contributes to discovering more vulnerabilities (12 vs. 5) and producing more code coverage (18.9% vs. 3.8%) on the CQE dataset than the concolic execution in Driller.

Outline

Question: How to combine fuzzing and concolic execution

  1. Demand launch: Driller, hybrid concolic testing

    Fuzzing starts first and concolic execution is launched only when fuzzing cannot make any progress for a certain period of time, a.k.a., stuck

  2. Optimal Switch

    Quantify the costs for exploring each path by fuzzing and concolic execution respectively and choose the more economic method for exploring the path

Drawback of exsiting strategy

Athough existing strategies sound intriguing, none of them work adequately, due to unrealistic or oversimplified assumptions.

  1. Demand Launch
    • Fuzzing is making progress does not necessarily mean concolic execution is not needed.
    • This strategy does not recognize specific paths that block fuzzing. Once the fuzzer gets stuck, the demand launch strategy feeds all seeds retained by the fuzzer to concolic execution for exploring all missed paths
  2. Optimal Switch
    • Nontrivial to quantify the costs of fuzzing and concolic execution for each path
    • Hard to normalize the cost of concolic execution and fuzzing for a unified comparison, because these two costs are estimated by techniques with different metrics.

Novelty: Design principle for building a hybrid fuzzing system

  1. Let concolic execution solve the hardest problems
  2. Let fuzzing take the majority task of path exploration
  3. Extra analysis must be lightweight to avoid adverse impact on the throughput

Discriminative dispatch: Prioritize paths so that concolic execution only works on selective paths that are most difficult for fuzzing to break through

Key Challenge: How to quantify the difficulty level for each path

  1. Existing work perform expensive program analysis to evaluate the difficulty
    • symbolic execution
    • value analysis
  2. Quantify a path’s difficulty by its probability of how likely a random input can traverse this path.
    • Treat fuzzing as a random sampling process
    • Calculate each path’s probability based on the sampling information.

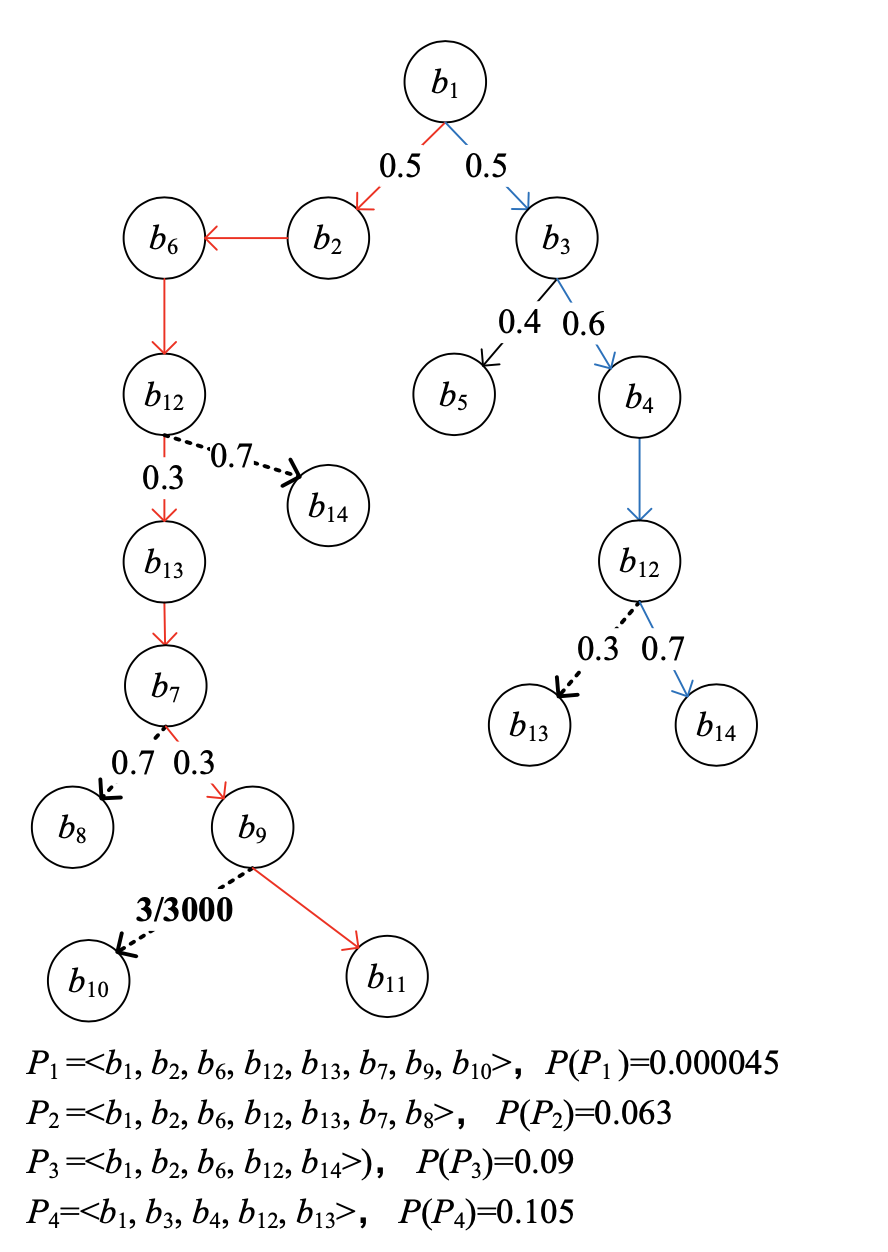
Theoretical Model: Monte Carlo

Calculate the probability of a path to be explored by fuzzing.

Fuzzing could fulfill two requirement of conducting Monte Carlo method:

  • fuzzing randomly generate inputs for testing programs => sampling to the search space is random
  • fuzzing has a very high throughput => a large number of random sampling for estimation

How to calculate the probability for each branch

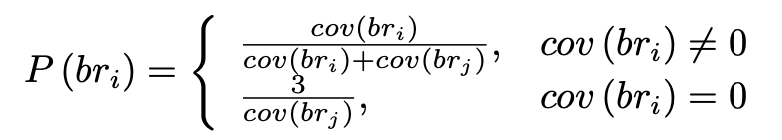
image-20210603221145158

How to calculate the probability of each path

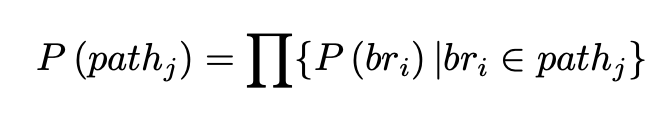
image-20210603221825939

Implementation: DigFuzz

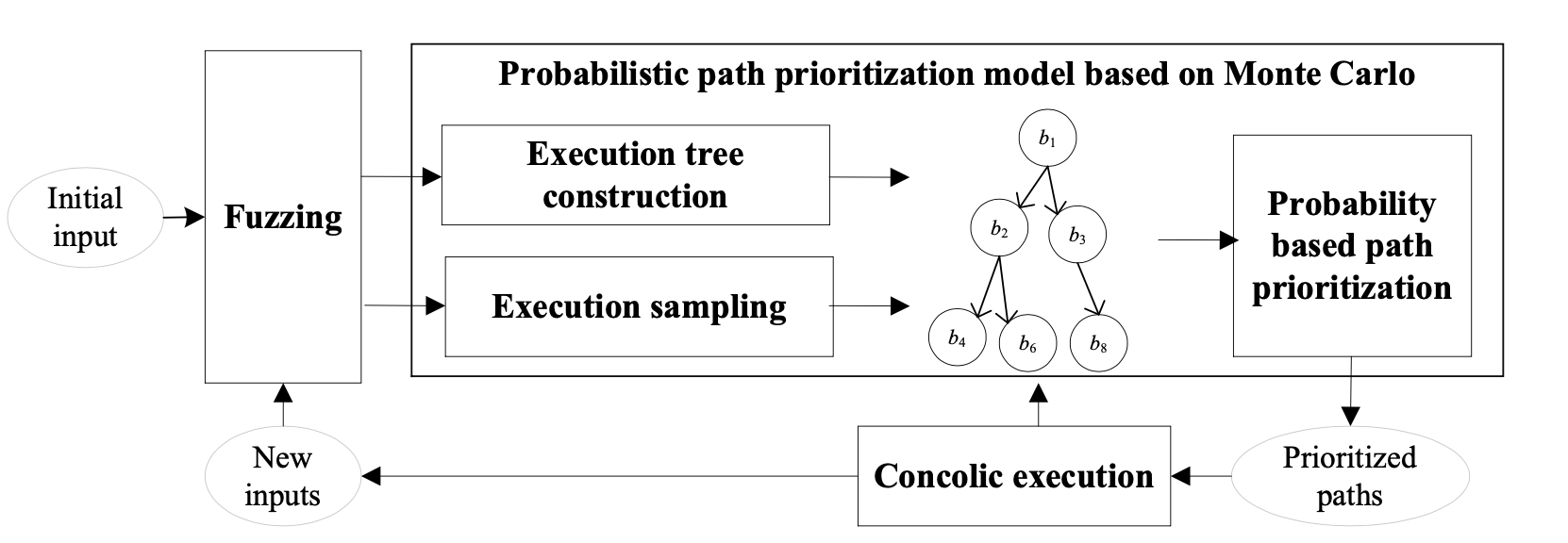
image-20210603222727877

Step 1: Execution Sampling

Input: Program, Fuzzer, Initial Seed

Output: HashMap of Coverage, Corpus

Perform execution sampling to collect coverage statistics which indicate how many times each branch is covered during the sampling.

Step 2: Execution Tree Construction

Input: Control flow graph, HashMap of Coverage, Corpus

Outputput: Execution Tree with Prob

Note: Only perform trace analysis for seed ratained by fuzzing to avoid path explosion

Step 3: Probabilistric Path Prioritization

Input: Execution Tree

Output: A set of missed paths and their probability

Prioritizes all the missed paths in the tree, and identifies the paths with the lowest probability for concolic execution.

image-20210604173949532

Evaluation

DataSet: CQE, LAVA-M

Metrics: coverage, vulnerability, contribution of concolic execution